BioNTech-Pfizer COVID-19 Vaccine Candidate Efficacy

Yesterday (Nov. 9, 2020), BioNTech and Pfizer announced results from an interim analysis of their RNA-based COVID-19 vaccine candidate. The analysis was based on 94 confirmed cases and concluded the vaccine candidate was more than 90% efficient. The study has enrolled 43,538 participants but only 38,955 participants have received both doses.

Although the full results haven’t yet been published, we can make some assumptions and infer some information. The study protocol (PDF) specifies a 1:1 randomization between the treatment (vaccine candidate) and control group (placebo), and no serious safety concerns have been reported. Thus we can expect about 19,477 in each group.

To achieve at least 90% efficacy in the vaccine candidate the treatment group could have as many as 8 participants with confirmed COVID-19 cases (and thus 86 cases in the control group).

Based on these inferences, I fit a model to recover the posterior distribution for VE (vaccine efficacy). The model samples from binomial distributions with beta priors to fit the number of cases for each of the treatment and control groups. The prior was taken from the study protocol and has been discussed here.

The Stan model code is below.

data {
  int N1;  // treatment group
  int y1;
  int N2;  // control group
  int y2;
}
parameters {
  real<lower=0, upper=1> theta1;
  real<lower=0, upper=1> theta2;
}
model {
  theta1 ~ beta(0.700102, 1);  // prior from study protocol
  theta2 ~ beta(0.700102, 1);
  y1 ~ binomial(N1, theta1);
  y2 ~ binomial(N2, theta2);
}
generated quantities {
  real riskratio = theta1 / theta2;
  real oddsratio = (theta1 / (1 - theta1)) / (theta2 / (1 - theta2));
  real efficacy = (theta2 - theta1) / theta2;
}

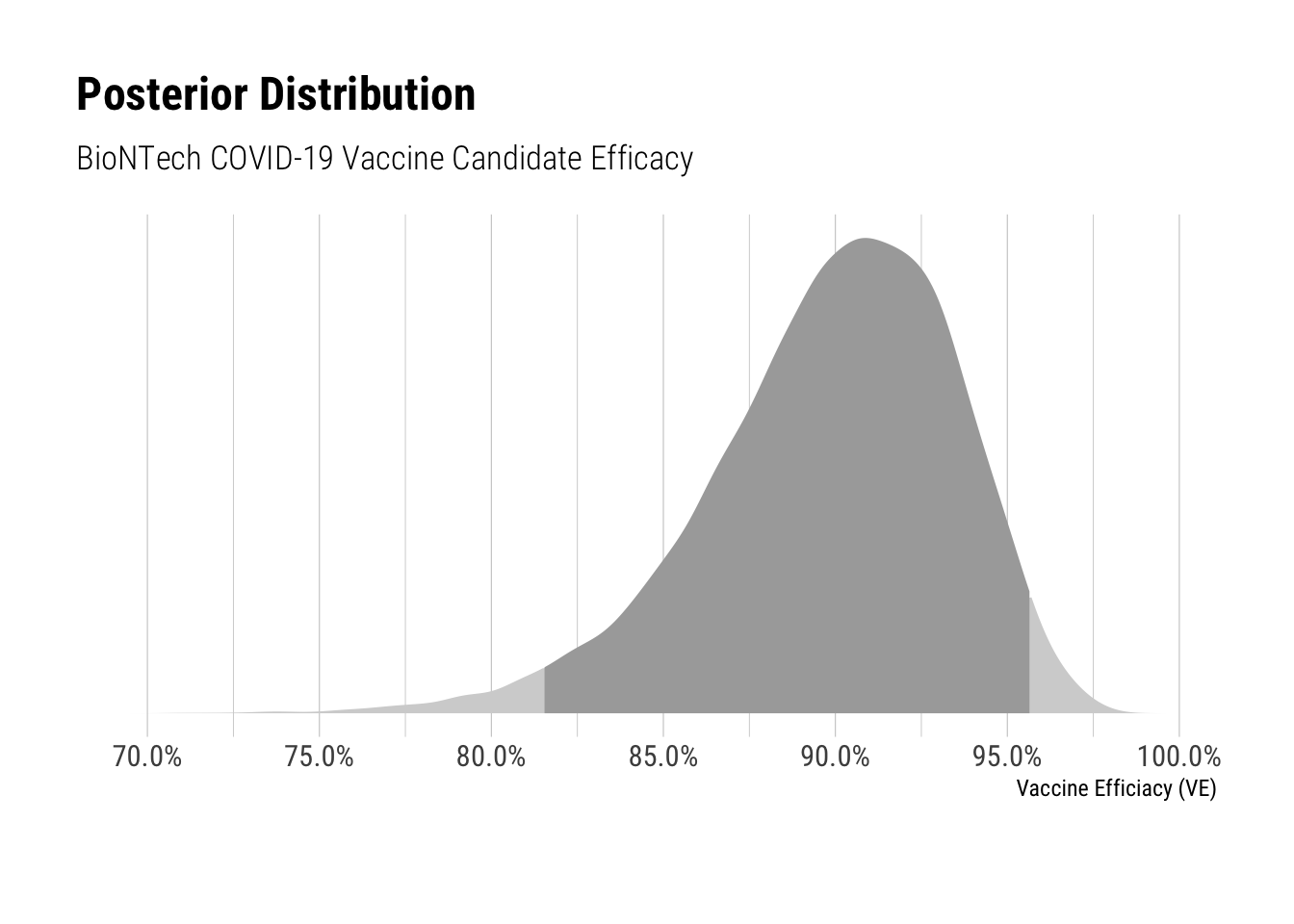
The vaccine candidate efficacy’s credible interval ranges from 81.6% to 95.6%. The posterior median is 90.3%, which is consistent with the reported efficacy. However the lower bound is nearly 10% lower than the reported efficacy – demonstrating that later estimates of the vaccine candidate’s efficacy could be noticably lower.

Vaccine efficacy has implications for the extent of vaccine coverage needed for herd immunity to be effective. This is especially true if immunity is only conferred temporarily. Fortunately efficacy greater than 80% would seem to be adequate for effective herd immunity.