COVID-19 Risk by Incidence Rate and Event Size

The COVID-19 Event Risk Assessment Planning Tool provides county-level information about the probability that at least one person in a group would be infected with COVID-19. The probability can be calculated as \[ \text{Pr(at least one person with COVID-19)} = 1 - (1 - \theta)^n \] where \(\theta\) is the local incidence rate and \(n\) is the number of people at the event.

While we can’t directly control the incidence rate, we can control the number of people we’re exposed to via the event size. If we determine an acceptable level of risk we can then solve for \(n\) to see the maximum event size by rewriting the equation above as

\[ n = \text{floor} \left( \frac{\text{log}(1 - \pi)}{\text{log}(1 - \theta)} \right) \] where \(\theta\) is the incidence rate and \(\pi\) is the acceptable level of risk. For example if the local incidence rate is 2% and you’re comfortable attending an event with a 10% chance that an attendee has COVID-19 then the maximum event size is 5 people.

We can also plot the risk level by incidence rate and event size which allows us to see how low the incidence rate would need to be to attend an event with a certain level of risk.

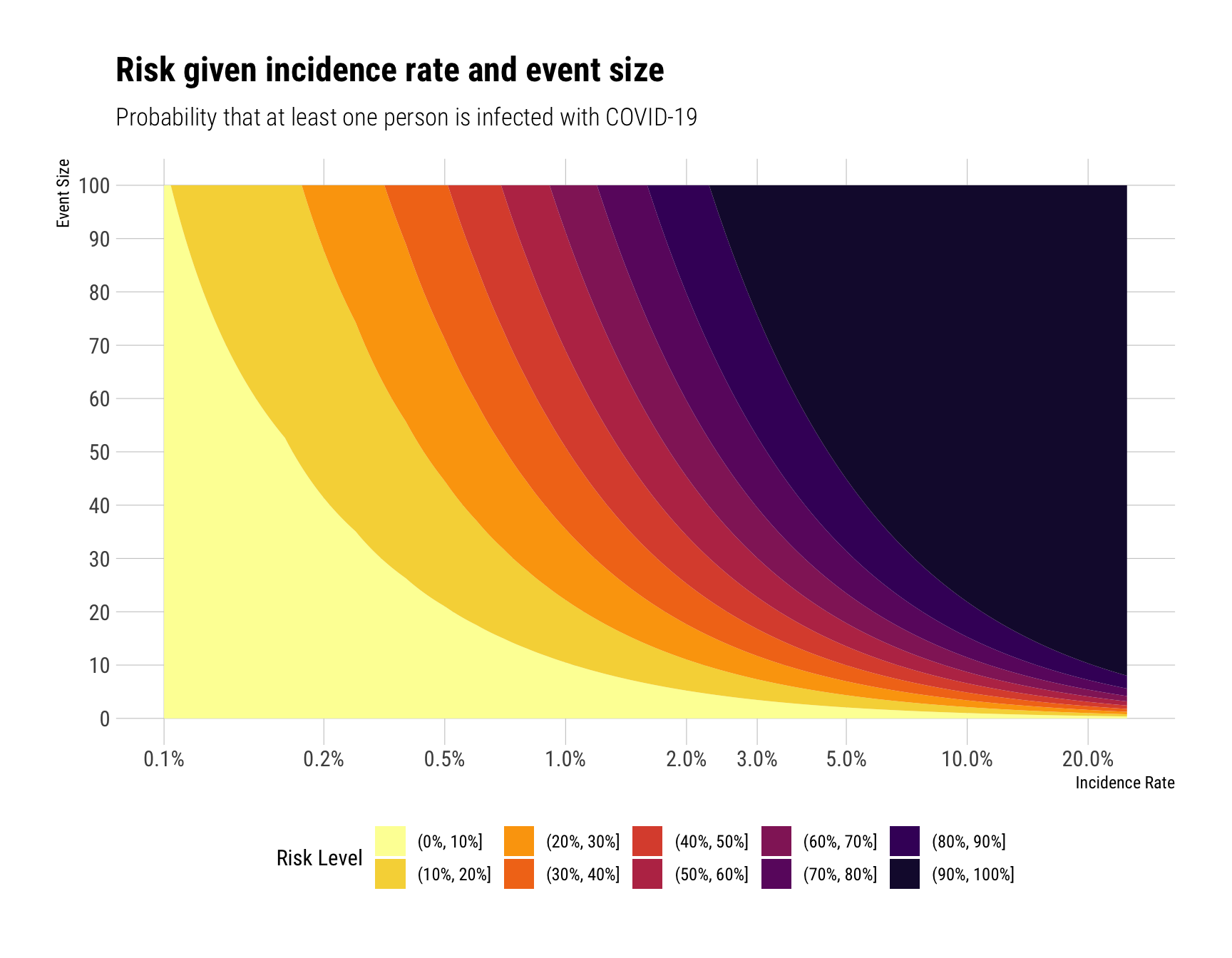
It is important to remember that these equations treat risk as being homogeneous within a population but risk for COVID-19 is heterogeneous. This is a simplification in which risk is uniformly distributed throughout the population. However socializing in a gathering in a group of 5, in which all participants have self-isolated for 10-14 days and exhibit no symptoms has an inherently different risk than attending a gathering with random members of the population. Attending an event in which at least one attendee has COVID-19 does not guarantee but significantly increases your chances that you will become infected. Because risk of infection is gated by exposure, and because people enjoy socialization, it is useful to understand risk of exposure given the incidence rate and event size.